OR-Tools 從小白到入門

前面介紹了 OptaPy 與 OptaPlanner 求解器（暫時下架整改），這篇談的則是另一款由 Google 出品的求解器 OR-Tools，為了文章的完整性，在進入 OR-Tools 前，還是快速介紹一下什麼是規劃問題，以及什麼是求解器。

規劃問題與求解器

對一般用戶來說，他們可以在 LibreOffice Calc 等試算表中，建立一些公式及目標，然後使用求解器功能幫他們找出最接近目標的儲存格組合，例如「該怎麼找零才能不會讓顧客拿到一大堆硬幣？」這個問題在求解器的模型中，我們改以這種形式提問：「該怎麼組合各種幣值的鈔票與硬幣，好讓顧客拿到的貨幣數量是最少，並且金額是對的？」我們以下圖表達此問題：

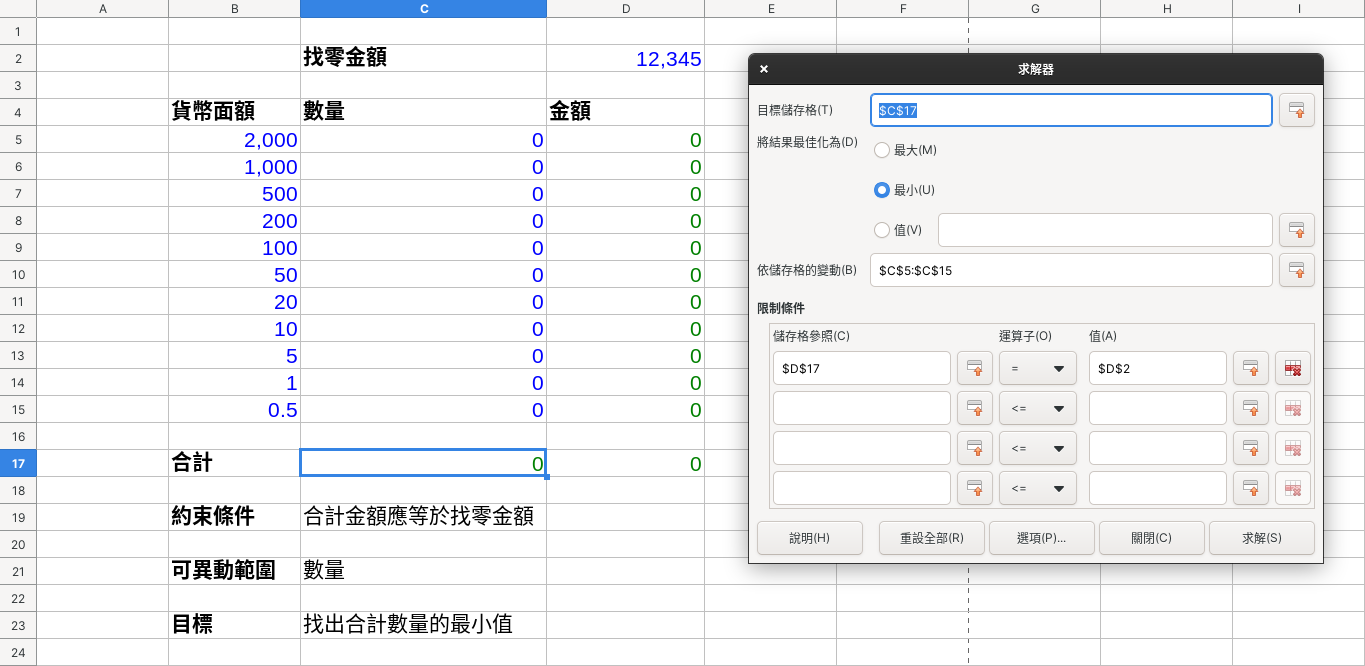
最後求出之解如下：

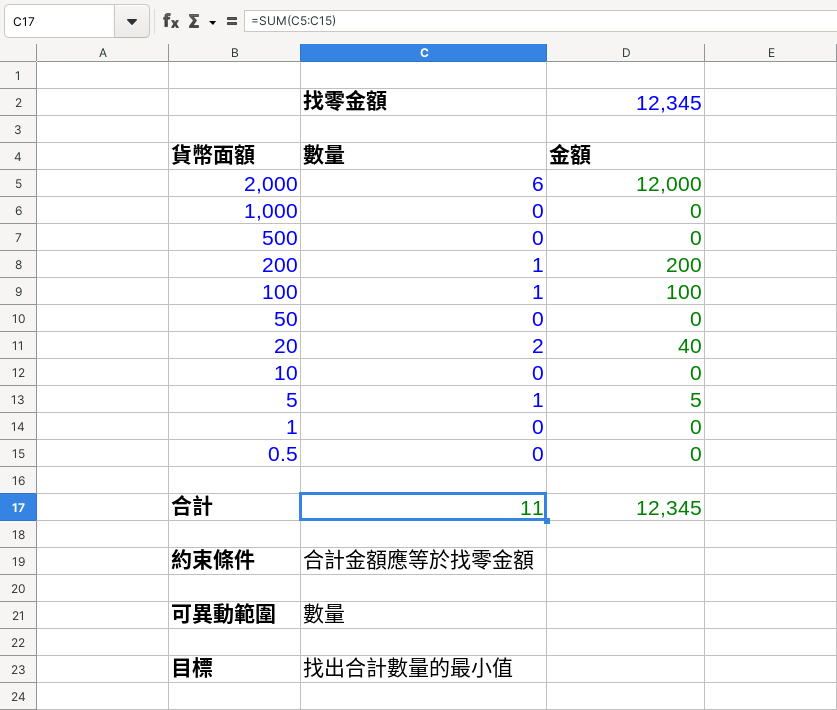
最終顧客拿到 11 個各式貨幣，並且金額正確（詳見〈認識求解器〉）。

像上面這樣的問題，屬於線性規劃問題，但還有一些更為複雜的問題，例如：

• 排班、排程、排工問題，怎麼排才能公平又滿足多方需求？
• 路徑規劃問題，怎麼走才能讓運輸效率最大化？
• 裝箱問題，怎麼裝才能讓箱體利用率最大化？
• 裁切問題，怎麼切才能讓物料利用率最大化？
• 賽事問題，怎麼排才能讓賽事公平而不強碰？
• 投資問題，怎麼配置才能讓收益最大化？

這些問題的共同特徵是「運算複雜、驗證簡單」，運算之所以複雜，是因為其中有近似無限種可能，舉例來說，暴走二人組要走遍全台灣所有鄉鎮市區，其中路徑就有幾乎無限種可能，而驗證之所以簡單，有沒有真的走遍全台灣，用座標就可以秒驗證。

對於這類問題，我們不太可能去窮舉所有可能性再找出最佳解，因為如此所耗費的時間可能是天文數字，但可以透過求解器來幫我們找出「近似最佳解」，在理論上之「真．最佳解」無法求得的情況下，近似最佳解已足夠滿足我們的需求。

OR-Tools

OR-Tools 是 Google 開發的求解器，名字中的「OR」表示 operations research（作業研究），這是一門科學化探討各種作業問題的學科。OR-Tools 本身是以 C++ 開發，另提供多種語言的 API，由於 C++ 可直接編譯成各平台的原生二進位檔，因此不像 OptaPy 那樣還要等 JVM 跑起來，OR-Tools 即使在世界知名的慢速語言 Python 下跑起來都可以秒解問題，既提高了效率，也減少了客怨。

OR-Tools 內集合了多個求解器，每個求解器就是一套演算法，它們各有擅長之處，有的適合解線性問題，有的適合解約束問題，因為本人的需求為約束問題，所以下面只會談到 OR-Tools 中的約束問題求解器 CP-SAT。

在 Python 安裝 OR-Tools 就是那永遠的 pip install：

$ pip install ortools

繼續閱讀

Share